Теплоперенос в плотном движущемся слое дисперсного материала при микроволновоконвективной сушке.

E-mail: a – boshkova.irina@gmail.com; b – natvolgusheva@gmail.com;
c – dorosh1gan@gmail.com; d – l_zharikova@mail.ru

Аннотация
В работе аналитически исследуется процесс переноса теплоты в движущемся плотном
слое. Представлена двухкомпонентная математическая модель процесса теплопереноса, которая включает уравнения энергии газового и твердого компонентов. Приведены результаты решения, полученные методом интегральных преобразований Лапласа. Учитывается два источника теплоты – положительный, от действия микроволнового поля и отрицательный, связанный с испарением влаги. Приведенные зависимости предлагается использовать для конструкторских и поверочных расчетов сушилок для зерна.

Применение микроволновой энергии позволяет достичь высоких скоростей сушки без
перегрева материала [1]. Одновременная продувка через слой сушильного агента обеспечивает не только дополнительный подвод теплоты, но и существенную интенсификацию процессов тепломассопереноса в слое. Математические модели микроволновой сушки приведены в [2, 3]. Математическая модель теплопереноса при сушке дисперсного материала в движущемся плотном слое при кондуктивно-конвективном теплоподводе приведена в [4]. Модели для комбинированного микроволново-конвективного подвода теплоты в литературе отсутствуют. Рассматриваются модели таких процессов для движущегося слоя, который используется в сушилках непрерывного действия. Рассмотрим сушилку, представляющую собой вертикальный канал, в который из загрузочного бункера поступает влажный дисперсный материал. В нижнем сечении канала расположено выпускное устройство, обеспечивающее движение материала в виде плотного слоя и его необходимый расход. В верхнем (входном) сечении канала размещены магнетроны, создающие заданный тепловой поток. Через это же сечение подается сушильный агент, который фильтруется сквозь слой и удаляется из нижнего (выходного) сечения. За счет поглощенной влажными частицами МКВ энергии и теплоты, передаваемой ему от сушильного агента путем межкомпонентного теплообмена, происходит прогрев частиц и испарение влаги, высушенный материал удаляется через выпускное устройство. Заданное влагосодержание на выходе обеспечивается выбором режимных характеристик: мощности магнетрона, температуры и скорости сушильного агента, скорости слоя и высоты канала. При формулировке модели теплопереноса используются следующие представления.
Плотный продуваемый слой рассматривается как двухкомпонентная система, состоящая из твердого (частиц) и газового (сушильный агент) компонентов, между которыми протекает
межкомпонентный тепломассообмен. МКВ энергия, поглощаемая частицами, учитывается
как положительный внутренний источник теплоты в твердом компоненте. На основании
экспериментальных данных [1] принято, что производительность этого источника убывает
по экспоненциальному закону по мере удаления от входного сечения, где подводится МКВ
энергия. Расход теплоты на испарение влаги учитывается, как отрицательный источник
теплоты в твердом компоненте. Производительность этого источника, зависящая от скорости сушки, остается неизменной на участке постоянной скорости и убывает по высоте канала по экспоненциальному закону на участке падающей скорости. Приняты следующие допущения:
• свойства компонентов неизменны, не зависят от температуры и влагосодержания;
•подводимая МКВ энергия, температуры и скорости компонентов распределены по сечению канала равномерно;
• температуры компонентов во входном сечении распределены равномерно;
• теплопотери через стенки канала пренебрежимо малы.
При таких условиях температуры компонентов будут изменяться только по высоте канала, т.е. температурные поля будут одномерными.
Математическая модель процесса теплопереноса включает уравнения энергии газового
и твердого компонентов и граничные условия. Эти уравнения для участка падающей скорости сушки имеют следующий вид (при пренебрежимо малом продольном переносе теплоты кондукцией):

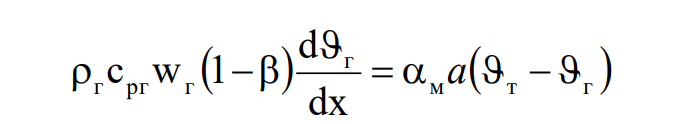
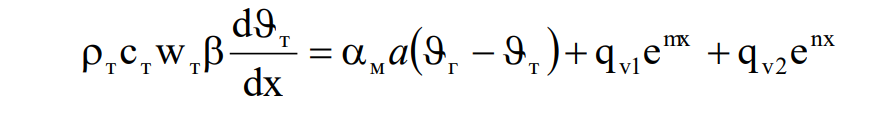
Граничные условия на входе:

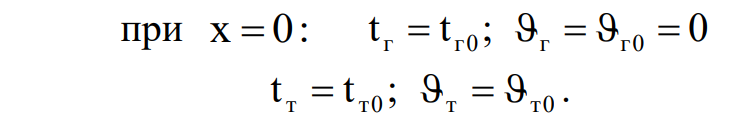
Производительность источника, обусловленного испарением влаги, определяется соотношением

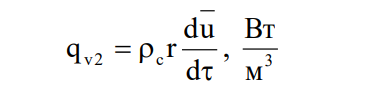
Решение системы уравнений (1, 2) с граничными условиями (3, 4) методом интегрального преобразования Лапласа позволило получить следующие зависимости для распределения температур компонентов на участке падающей скорости сушки:

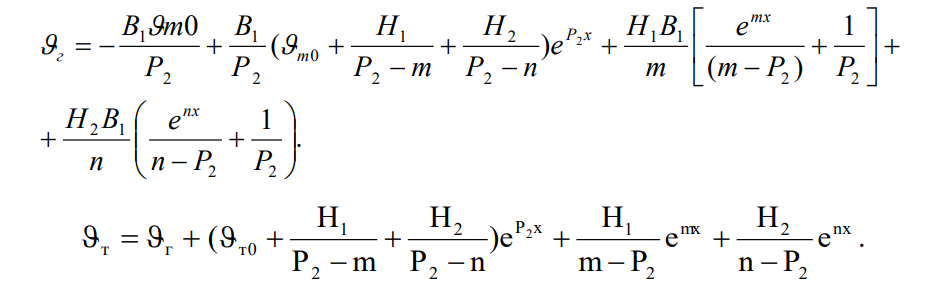
Здесь:

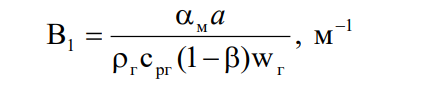
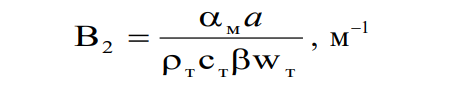
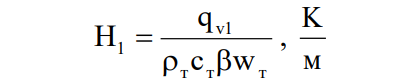
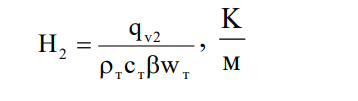
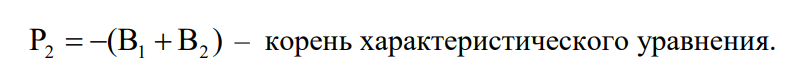
Как видно из (6, 7), температуры компонентов зависят от их физических характеристик,
скоростей, интенсивности межкомпонентного теплообмена, размера частиц, подводимого
потока МВ энергии, скорости сушки, координаты.
В одном и том же сечении, температуры компонентов различны. При x=idem разность
этих температур определяется выражением:

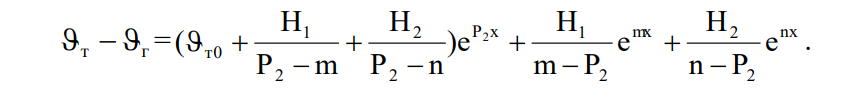
Она возрастает с ростом разности температур на входе (при x=0), производительности
источников, уменьшением абсолютного значения P2 . Из выражений (8, 9, 12) видно, что абсолютное значение P2 тем меньше, чем ниже тепловой поток, переносимый в процессе межкомпонентного теплообмена, по сравнению с тепловым потоком, переносимым компонентами конвекцией.
На участке постоянной скорости сушки распределения температур компонентов описываются зависимостями:

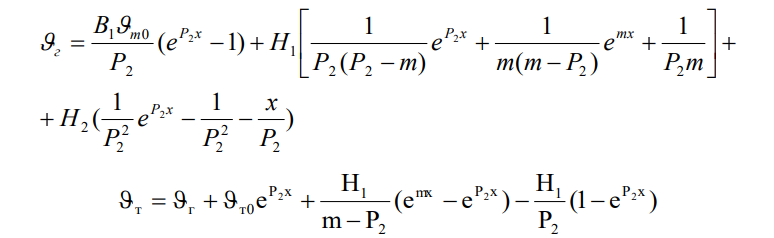
Возможны случаи, когда источник, обусловленный поглощением МВ энергии, также не
изменяется по высоте канала (m=0) (когда коэффициент ослабления потока энергии в слое мал либо магнетроны размещены в нескольких сечениях по высоте на небольших расстояниях друг от друга). В таких случаях уравнения (14, 15) приобретают вид:

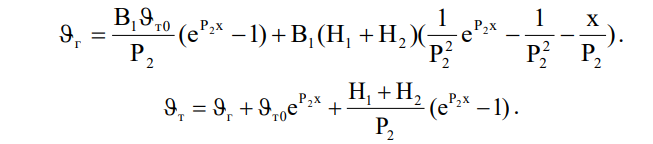
Если в слое отсутствуют внутренние источники, то температуры компонентов определяются только условиями межкомпонентного теплообмена и их изменение по высоте канала описывается зависимостями:

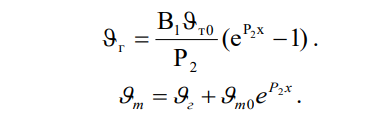
При режимах, в которых тепловой поток, обусловленный межкомпонентным теплообменом, существенно превышает тепловой поток, переносимый компонентами конвекцией, температуры компонентов при x=idem практически одинаковы
Рассмотрены также частные случаи – использование только одного способа подвода
теплоты (микроволнового либо конвективного).
Расчеты показали [5], что на начальном участке по высоте канала температура газа
уменьшается, а температура частиц увеличивается. Причем, в одном и том же сечении (при x=const) при увеличении мощности магнетрона, т.е. положительного внутреннего источника v1 q , и температуры газа и частиц и их разность возрастают.
При увеличении скорости газа происходит рост температуры газа и частиц (при x=const),
причем при разных скоростях газа частицы достигают большей температуры, чем газ.
Влагосодержание материала по высоте сушилки уменьшается. Как при увеличении
мощности магнетрона, так и при увеличении скорости сушильного агента происходит более интенсивное испарение влаги и уменьшение влагосодержания материала.
Приведенные зависимости позволяют выполнять конструкторские и поверочные расчеты
сушилок с движущимся слоем для различных дисперсных материалов при использовании
микроволновой энергии. При этом должны быть известны свойства и закономерности кинетики сушки конкретного материала при соответствующем способе подвода теплоты.

Список литературы

1. Календерьян, В. А. Исследование кинетики сушки крупы гречихи в микроволновом
   электромагнитном поле / В. А. Календерьян, И. Л. Бошкова, Н. В. Волгушева // ИФЖ. – 2006. – №3, Т. 79. – С. 123 – 127.
2. Лыков, А. В. Тепло- и массообмен в процессах сушки / А. В. Лыков. − М.-Л.: ГЭИ,− 464 с.
3. Календерьян, В. А. Влияние режимных параметров на распределение температур в
   движущемся плотном слое дисперсного материала при микроволново-конвективной сушке / В. А. Календерьян, И. Л. Бошкова, Н. В. Волгушева // Пром. теплотехника, 2010. − Т. 32, № – С. 37-44.
4. Сафин, Р. Р.Математическая модель конвективной сушки коллоидных капиллярнопористых материалов при давлении ниже атмосферного / Р. Р. Сафин, Р. Р. Хасаншин, Р. Г. Сафин. // Вестник Казанского технол. ун-та. – 2004. № 1. – С. 266-272.
5. Календерьян, В. А. Тепломассоперенос в аппаратах с плотным дисперсным слоем /
   В.А. Календерьян, И.Л. Бошкова // Монография. − К., 2011. – 184 с.